What are Blom Filters and when it makes sense to use them.
What is a bloom filter? It’s not a hot dog. (Silicon Valley 😂)
A bloom filter is a memory efficient data structure that allows inserting elements in a set and checking if an element already exists. It was developed and published by Burton Howard Bloom in 1970.
To start you can imagine a hashtable, which allows you to check if an element exists, using the key. The hashtable stores the key and the value of each element, but a bloom filter does not. That makes the bloom filter memory efficient but useless if you need to store the data, right? Not really. You can have the data stored in another data structure in-memory or in a database and also have the bloom filter to execute the “exists” operation without going through each element. This is particularly interesting when you have a large amount of data.
It is important to note that with this data structure it is possible to get false positives but false negatives never happen. As it is possible to get false positives, this data structure is probablistic and the “exists” operation has two possible outcomes:
- The element is possibly in the set.
- The element is definetely not in the set.
The key feature here is that there are no false negatives, ensuring there will be no duplicates when using a bloom filter. The probability of false positives will be briefly addressed later on.
But how does it work?
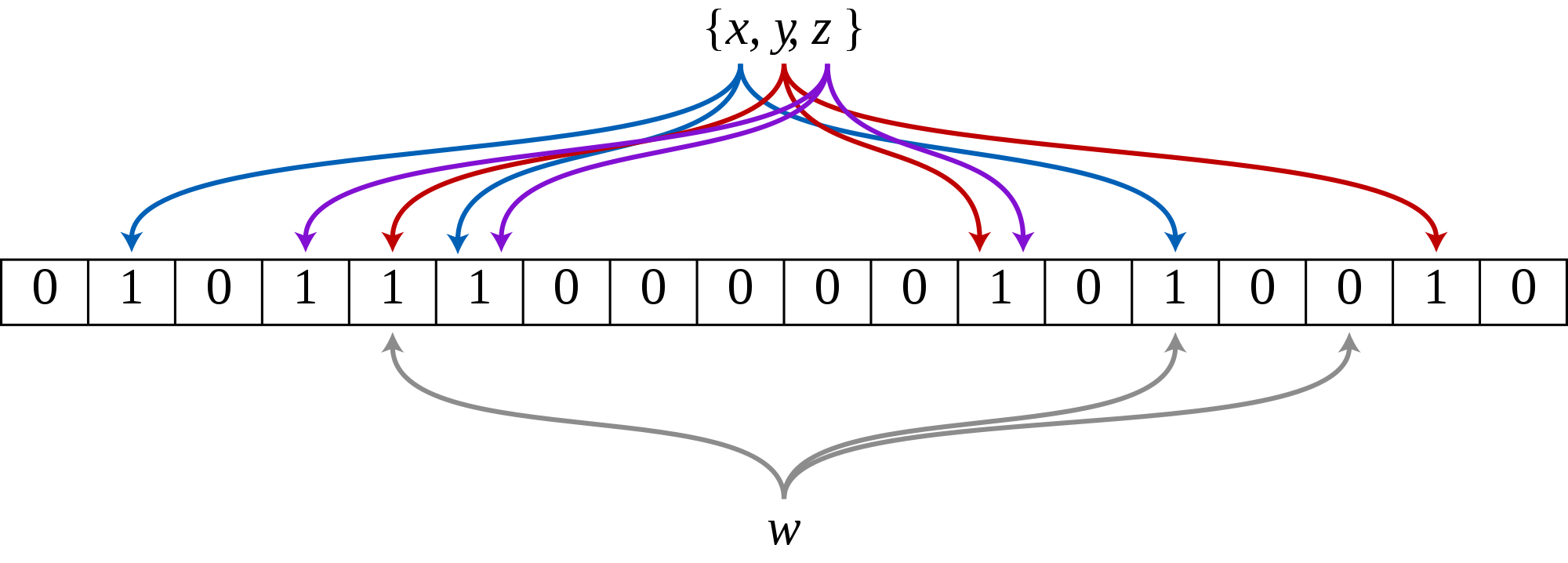
The bloom filter’s structure is very basic. It is just an array of m bits. It is also necessary to define/use k hash functions. These hash functions will be used to get k positions for each element that is inserted in the bloom filter. The output of the hash functions defines the positions in the array that will be set to 1.
When querying if an element exists, the same k hash functions are applied and if all the positions are set to 1, the algorithm will return “The element is possibly in the set”. In the following figure, you can see that m=16 and k=3. That means that there are 3 hash functions whose results are used to fill 3 positions of the buffer for each element. The top elements were inserted into the bloom filter and set the corresponding bits to 1. The w element is being used to query if it is already present in the set. The result here would be no because one of the bits is 0.
What is the probability of false positives? How many hash functions should I use?
Here I will just show you the formulas because this post is intended to be just an introduction to bloom filters.
If you are curious, you can check Wikipedia for a detailed proof.
The probability is defined by the following formula: (n=“Number of elements”)
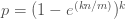
Given this probability, there is also an ideal number of hash functions to minimize it, depending on the size of the array and the number of elements.
It’s intuitive that if we use too many hash functions the buffer will be filled quickly and the collisions will increase. On the
other hand, if we use too few, it is also possible that the collisions increase because the chances of collision for the output of the hash functions are greater.
The ideal number of hash functions is defined by the following formula, considering m and the number of elements: (n=“Number of elements”)
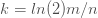
Removing elements
Removing items is not specified in the definition of a Bloom Filter. It is not hard to implement the removal of an element but probably you don’t want it, because removing one element might affect other elements. Removing an element would be done by setting all the bits in the corresponding positions to 0. Some of those bits might also have been set by other elements. So, by removing one element you might also be removing elements you don’t plan to.
Time complexity
Inserting and testing an element’s existence are constant-time operations, assuming O(1) hash functions.
Hope you enjoyed this post, suggestions are welcome. ☺